Trotz, dass die Regeln für Roulette so gestaltet sind, dass die Bank auf lange Sicht garantiert Geld verdient, ist Roulette eigentlich ein recht faires Spiel, wahrscheinlich sogar das fairste Spiel aller Glücksspiele. Wenn man nur mit geringen Beträgen (im Verhältnis zum Einkommen) spielt, kann man schön lange spielen und dabei richtig viel Spaß haben.
Wir schauen uns in diesem Artikel an, wie die Wahrscheinlichkeiten beim Roulette berechnet werden, einschließlich der Gewinnchancen für jede Wette.
Wahrscheinlichkeiten Fachchinesisch – Eine superkurze Einführung
 Collage von Shutterstock-Bildern;
Collage von Shutterstock-Bildern;Vordergrund: Donskarpo,
Hintergrund: Nata789
Nehmen wir das klassische Beispiel eines Würfels mit den Zahlen eins bis sechs. Wie groß ist die Wahrscheinlichkeit, dass der nächste Wurf die Nummer (genau) vier ist?
Die Antwort lautet: 1/6 oder 16,67%. Denn nur eine Seite des Würfels hat die Nummer vier, eine von insgesamt sechs Zahlen.
Und wie groß ist die Wahrscheinlichkeit, eine Zahl zu erhalten, die mindestens vier beträgt?
Die Antwort lautet: 50%. Es gibt drei mögliche Würfe (die Zahlen vier, fünf und sechs), was eine Chance von drei zu sechs (3/6) oder 1/2 bedeutet.
Beispiel verstanden? Wenn man von Wahrscheinlichkeiten spricht, macht es einen großen Unterschied, ob man über ‚genau‘ bzw. ‚mindestens‘ oder von irgendwas Anderem spricht. Der Teufel liegt bei Wahrscheinlichkeiten im Detail und darauf will dieser Artikel aufmerksam machen.
Roulette-Wahrscheinlichkeiten und die Mathematik dahinter: 36 Zahlen und die Null
Roulette hat insgesamt 36 Zahlen, 1 bis 36. Diese Nummern sind auf drei verschiedene Arten in jeweils gleich große Zahlengruppen zu je 18 Nummern unterteilt:
- 18 rote Zahlen (Rouge, engl. Red) und 18 schwarze (Noir, engl. Black)
- 18 gerade Zahlen (Paar, engl. Even) und 18 ungerade (Impair, engl. Odd)
- 18 Zahlen in der unteren Hälfte (Niedrig, Manque, engl. 1-18) und 18 in der oberen Hälfte (Hoch, Passe, engl. 19-36)
Im Gewinnfall erhält man einen Gewinn i.H.v. 1 : 1 ausgezahlt (50/50)
Klingt ‚fair‘. Nicht?
Aber! Es gibt es noch eine eigenständige Nummer, die grüne „Null“, was dann statt der 36 Zahlen, 37 nummerierte Zonen ergibt. Die Null ist jedoch in keinem der drei obigen Sätze enthalten.
Wenn man einen der drei Sätze spielt, also
- Rot oder Schwarz
- Ungerade oder Gerade
- Niedrig oder Hoch
…und die Wette gewinnt, erhält man seinen Einsatz zurück, plus 100%. Man verdoppelt sein Geld, da die Wettquote für jedes dieser Sets eine „Gleichheitswette“ ist (50/50).
Allerdings ist die Gewinnwahrscheinlichkeit, durch die Null, jeweils nur 18/37 = 48,65% und nicht 50%! Diese scheinbar kleine Differenz macht die Roulette Spieltisch Besitzer reich und nicht den Spieler und wird ‚Bankvorteil‘ genannt.
Durch die Null sichern sich Kasinos, dass sie immer auf der Gewinnerseite sind.
Übrigens, Roulette eignet sich fantastisch, um ein Gefühl für Wahrscheinlichkeiten zu entwickeln. In der heutigen Online Welt kann man Roulette am Computer spielen und mit einem virtuellen Guthaben (Bonus) muss man keine echten Verluste befürchten (sofern man natürlich nicht gierig wird und diszipliniert bleibt). Alles, was man dafür braucht, ist ein Online-Kasino, welches man über eine Vergleichsseite auswählen kann.
Es gibt eine große Auswahl an Roulette Variationen. Die klassische Variante ist das Französische Roulette: 36 Zahlen und eine Null, mit welcher das Haus (ohne Einsatz) immer gewinnt. Dieser Artikel zeigt die Berechnungen der Wahrscheinlichkeiten für diese Roulette-Art.
Der immerwährende Bankvorteil von Kasinos
Stellt man sich vor, dass die Häufigkeit der Ergebnisse einheitlich ist (d.h. jede Zahl erscheint einmal in 37 Umläufen), gewinnt die Bank jede 37. Runde, wenn die grüne Null eintrifft. Somit verlieren die Spieler durchschnittlich 1/37 ihres Einsatzes (vorausgesetzt natürlich, sie spielen immer mit dem gleichen Einsatz pro Runde).
Etwas anders erklärt:
- Der Spieler setzt gleichzeitig auf die Sätze „Rot“ und „Schwarz“.
- Simplifiziert gesprochen, der Roulette-Ball landet 36 von 37 Mal auf einer Zahl von eins bis 36.
- Da der Spieler auf alle 36 Zahlen gesetzt hat, verliert er jedes Mal eine der beiden Wetten, erhält jedoch die volle Entschädigung für die andere Wette. In Effekt: ein Nullsummenspiel.
- Der Spieler verliert jedoch beide Wetten, wenn der Ball auf der Null landet, und genau dies ist in 1/37 der Spiele der Fall.
Ein siebenunddreißigstel mag nicht zu schlimm klingen, aber wir rechnen mal ein wenig weiter, um den Hausvorteil vom Kasino uns richtig vor Augen zu führen.
Der Roulette Spieler kann bei einer einfachen Chance eine Rendite von 36/37 seines Einsatzgeldes erwarten. Dies entspricht einem erwarteten Wert i.H.v. 97,3%. Mit anderen Worten ausgedrückt, für 100 gesetzte Einheiten (100 €) erhält der Spieler durchschnittlich 97,3 Einheiten (97,30 €) zurück.
Wer-auch-immer das Roulette erfunden hat, war ein Genius. Das Tableau ist in einer Art designet, dass egal wie die gespielte Kombination ist, die Bank IMMER einen 2,7%igen Vorteil hat.
Dies ist nicht offensichtlich, und wir schauen uns das daher mal etwas genauer an.
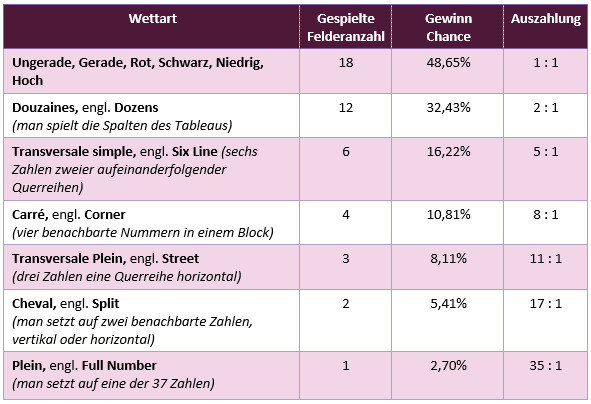
Wahrscheinlichkeitstabelle für Roulette-Wetten:
Beispiel des Bankvorteils bei der ‚Rot, Schwarz‘ Wette:
Es gibt 2 Sätze, die man spielen kann: Rot oder Schwarz. Die Chance, eine der beiden zu gewinnen beträgt 48,65%.
Ich hatte ja bereits weiter oben im Artikel erklärt, wie das berechnet wird. Die Gewinnwahrscheinlichkeit, durch die Null, beträgt jeweils 18/37 = 48,65%
Die Bank zahlt diese Wette 1 : 1 aus: 50% + 50% = 100%
Der Bankvorteil beträgt: 100% minus 97,3% = 2,7%
Beispiel des Bankvorteils bei der ‚Transversale plein‘ Wette:
Bei der Transversale plein (Street) spielt man eine Querreiche horizontal (3 Zahlen). Die Chance, das die Querreihe gewinnt, beträgt 8,11%.
Es gibt insgesamt 12 Querreihen:
8,11% x 12 (Querreihen) = 97,3%
Die Bank zahlt diese Wette 11 : 1 aus: 12 x 8,33% = 100%
Der Bankvorteil beträgt: 100% minus 97,3% = 2,7%
Man kann jede Roulette Wette nachrechnen und es sind IMMER 2,7% Bankvorteil. Bei jeder Wette. Die Gewinnquoten für die Wetten sind so berechnet, als ob die Null nicht vorhanden wäre, d. h. als ob es nur 36 statt 37 Zahlen gäbe. Die Ausschüttungsquote beträgt somit immer 97,30 %.
Trotz dieses eindeutigen mathematischen Bankvorteils glaubt fast jeder Roulette Spieler, dass es Gewinnsysteme gibt, mit denen man beim Roulette ‚garantiert‘ gewinnen kann. Wir schauen mal kurz auf den gängisten Irrglauben.
Erwartete Sequenzen für einfache Wahrscheinlichkeiten
Lieber Leser, bist du auch eine der Personen, die daran glaubt, dass, wenn du fünfmal hintereinander ‚Rot‘ siehst, die Wahrscheinlichkeit für ein ‚Schwarz‘ steigt?
Viele glauben, dass die Chancen für „Schwarz“ jetzt höher sind. Schwarz ist schon eine Weile nicht mehr aufgetaucht, also muss es sicher bald wieder eintreffen, um die Frequenz auszugleichen.
Falsch. Selbst nach fünfmaliger Folge von „Rot“ bleibt die Wahrscheinlichkeit für Schwarz immer gleich: 18/37 = 48,65%. Das Roulette Rad hat kein Gedächtnis – es weiß einfach nicht, was die letzte Zahl war.
Deshalb macht es keinen Sinn, die Folge von Rot und Schwarz aufzuschreiben. (Wer hat noch keine Spieler in Kasinos beobachtet, die sich dieser Gewohnheit verschrieben haben?). Es ist unmöglich, auch nur die kleinsten Muster im Roulette-Rad zu erkennen. Der Ball hat kein Gedächtnis und jede Drehung des Roulette Rads gibt eine neue zufällige Zahl heraus. Punkt.
So gering die Wahrscheinlichkeit, dass „rot“ sechs Mal hintereinander erscheint, so gering auch die Wahrscheinlichkeit, dass es fünfmal hintereinander rote Zahlen gibt, gefolgt von einer schwarzen Zahl.
Die Chance von sechs Rot in einer Reihe ist:
Die Chance von fünf Rot in einer Reihe gefolgt von Schwarz ist:
Dies ist übrigens ungefähr die Hälfte der Wahrscheinlichkeit, dass eine einzelne Zahl erscheint, beispielsweise eine Fünf (1/37 = 2,7%).
Beispiele für Wahrscheinlichkeiten
Hier ein paar mehr Beispiele, um ein besseres Gefühl für die Roulette-Wahrscheinlichkeiten zu entwickeln.
Wir verwenden „r“ für Rot und „s“ für Schwarz:
r oder s: 18/37 = 48,65%
rr oder ss: 18/37 x 18/37 = 24% (zwei rote in einer Reihe oder zwei schwarze in einer Reihe)
rs oder sr: 36/37 x 18/37 = 47,3% (eine Farbe gefolgt von der anderen)
rrr oder sss: 18/37 x 18/37 x 18/37 = 11,5%
rsr oder srs: 18/37 x 18/37 x 18/37 = 11,5%
rrrr oder ssss: 18/37 x 18/37 x 18/37 x 18/37 = 5,6%
Man darf diese Wahrscheinlichkeiten niemals mit den „bedingten Wahrscheinlichkeiten“ verwechseln.
Die Wahrscheinlichkeit, dass eine Person vier Mal hintereinander ‚rot‘ sieht, beträgt 5,6% (siehe Berechnung oben).
Wenn jemand jedoch unmittelbar nach dem Erscheinen einer roten Zahl an den Roulette Tisch kommt (diese Runde aber nicht gesehen hat), ist die Wahrscheinlichkeit, dass er/sie drei ‚rot‘ sieht beträgt 11,5 %. Dies ist, weil diese Person nur eine Serie von drei Runden beobachten wird und nicht vier, wie die andere Person.
Wer etwas mehr über Wahrscheinlichkeiten und Kombinatorik lesen möchte, hier ist ein anderer Artikel dazu: Praktische Anwendung von Kombinatorik beim Fußball Wetten
Das Gesetz der kleinen Zahlen
Das Gesetz der kleinen Zahlen wurde erstmals 1898 von Ladislaus Bortkiewicz (1868-1931) beschrieben. Dieses Gesetz ist nicht gerade ein Lesematerial zur Schlafenszeit, aber hier ist eine kurze Zusammenfassung.
Da Roulette ein Spiel von Wiederholungen ist, werden das „Gesetz eines Drittels“ und das „Gesetz von zwei Dritteln“ im Spielverlauf offensichtlich.
Wenn beim Roulette genau 37 Umdrehungen ausgeführt werden (so viele wie es unterschiedliche Zahlen gibt), werden, lt. dem Buch:
- Etwa ein Drittel der Zahlen (ungefähr 12-15 Zahlen) überhaupt nicht getroffen
- Etwa ein Drittel der Zahlen erscheint genau einmal
- Etwa ein Drittel der Zahlen erscheint zweimal oder öfter
- Etwa zwei Drittel der Zahlen werden mindestens einmal angezeigt
⇨ Welche Zahlen konkret, das steht allerdings in den Sternen geschrieben.
Ist spannend. Nicht? Dies ist ein Roulette Spiel wert.
Ins Kasino gehen und 37-mal auf seine Lieblingszahl setzen. Während das Rad gedreht wird, sich die Nummern aufschreiben, um das Gesetz der kleinen Zahl zu überprüfen und wenn man Glück hat, gehört die Lieblingszahl zu dem Drittel, welches mehr als einmal erscheint, und man verlässt das Kasino mit etwas Cash.
Das Gesetz der großen Zahlen
Das Gesetz der großen Zahlen besagt, dass die tatsächlich beobachtete Frequenz mit einer Zunahme der Wiederholungen den theoretisch berechneten Wahrscheinlichkeiten nahekommt.
Obwohl es beispielsweise durchaus möglich ist, dass an einem bestimmten Abend 60-mal hintereinander nur rote Nummern auftauchen, und an einem anderen Abend 40-mal Schwarz hintereinander, wird letztendlich, wenn man das Roulette Rad über einen längeren Zeitraum beobachtet, beispielsweise einen Monat, die Gesamtverteilung von Rot und Schwarz näher an 50:50 sein.
Diese beiden Gesetze, das der kleinen und das der großen Zahlen, sind der Grund, dass es kein einziges Roulette-System gibt, mit welchem man die Wahrscheinlichkeiten, also das Haus, schlagen könnte. Es mag durchaus für eine kurze Zeit scheinen, dass ein bestimmtes System funktioniert, aber auf lange Sicht verliert man mit jedem System Geld. Die 2,7% Bankvorteil des Hauses sind ein Fakt und das Kasino verdient gutes Geld damit. Oder hast du schon mal ein armes Kasino gesehen?
Trotzdem macht Roulette spielen Spaß und da die Runden bei Roulette schön schnell hintereinander gespielt werden, ist es ein fantastisches Spiel, um sein Gefühl für Wahrscheinlichkeiten zu trainieren! Man sollte nur nicht dem Irrglauben folgen, dass man damit Geld verdienen kann. Das Kasino ja, aber nicht der Spieler. Punkt.