
Vergleich der erwarteten Resultate mit den bisher beobachteten Ergebnissen
An dieser Stelle vergleichen wir die erwarteten Resultate (= die durchschnittlich gespielten Ergebnisse von 5 Jahren) mit den bisher erzielten (= beobachteten) Ergebnissen der 2010/2011 Saison:
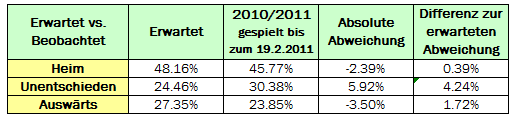
Es gibt auffallend große Abweichungen der beobachteten Ergebnisse in Unentschieden und Auswärts zu den Erwartungswerten. Ich bin mir jedoch ziemlich sicher, dass sich dass zum Saisonende hin ausgleichen wird, da ich denke, dass die Differenz damit begründbar ist, dass ich die statistischen Zahlen einer ganzen Saison mit Zahlen einer halben Saison verglichen habe. Diese Abweichung in Unentschieden und Auswärts deutet daher m.A. ziemlich eindeutig darauf hin, dass die gespielten Ergebnisse über’s Jahr unterschiedlich verteilt sind, je nachdem ob die Spiele am Anfang, in der Mitte oder am Ende einer Saison stattfinden.
Das heißt, wenn die Einzelquoten eines Spiels kalkuliert werden, muss dieser saisonale Effekt berücksichtigt werden. Für diesen Artikel und für das allgemeine Verständnis spielt das jedoch heute keine Rolle.
Durchschnitt (Mittelwert) und Absolute und relative Abweichung (Fehler)
Für diejenigen, die Schwierigkeiten haben zu verstehen, was ein Durchschnitt und eine Abweichung sind, hier noch ein paar zusätzliche Erklärungen mit Beispielen:
- Durchschnitt
Der Durchschnitt wird in der Statistik sowie umgangssprachlich synonym für den arithmetischen Mittelwert (das Mittel) benutzt. Der Mittelwert wird bei der Berechnung der Abweichung als „bekannter Wert“ (Erwartungswert) für Vergleichszwecke benutzt.
Beispiel Heimspiele:
(50.53% + 47.89% + 46.32% + 45.29% +50.79%) geteilt durch 5 = 48.16% - Absolute und relative Abweichung (Fehler)
Die absolute Abweichung wird in der Stochastik auch als absoluter Fehler bezeichnet.
Absolute Abweichung am Beispiel Heimgewinn 2005/2006:
50.53% (Ergebnis 2005/2007) minus 48.16% (Mittelwert) = 2.37% (Absolute Abweichung)Es gibt auch noch den Begriff der relativen Abweichung, welcher die prozentuale Abweichung zwischen dem beobachteten Wert (den Ergebnissen eines konkreten Jahres) und dem Erwartungswert (Durchschnitt aller Jahre) ist. Die relative Abweichung ist eine Normierung auf den Mittelwert und dient als Kenngröße, um auszudrücken, um wieviel Prozent die beobachteten Einzelergebnisse um den Mittelwert herum schwanken.
Relative Abweichung am Beispiel Heimgewinn 2005/2006:
2.37% (Absolute Abweichung) geteilt durch 48.16% (Mittelwert) = 4.92% (Relative Abweichung)
Es wird also „erwartet“, dass in der 2010/2011 Saison 48.16% aller Spiele mit einem Heimsieg enden.







Könnte man so auch Quoten für einzelne Mannschaften errechnen? Indem man guckt wie einzelne Mannschaften z.B. Bayern München zuhause gespielt hat, statt wie oben im Beispiel die gesamte Liga? Um die Heimquote für Bayern zu berechnen, würden wir dann die Durchschnittlichen Siege zu Hause nehmen + die Auswärtsniederlagen des gegners und dann die relative Abweichung einbauen? Möglich? oder Ansatz Falsch?
Hallo Sam,
ja, nicht nur „könnte“ man so auch Quoten für einzelne Mannschaften errechnen, sondern, man errechnet diese genau so! Man schaut wie einzelne Mannschaften z.B. Bayern München zuhause, spielen, und kombiniert das mit den Team, gegen das sie antreten. Um dann die Heimquote zu berechnen, nehmen wir dann die durchschnittlichen Siege zu Hause + die Auswärtsniederlagen des Gegners und bauen die relative Abweichung ein. Ja, total korrekt geschlussfolgert!
Dein Kommentar sagt mir jedoch, dass du nicht im Besitz meines Kurses (Wettkurs – Wetten auf Mehr als / Weniger als X Tore) bist. Liege ich da richtig? Denn in diesem geht’s um die Quotenberechnung für einzelne Mannschaften. Ich erkläre da lang und breit wie man das alles rechnet. Im Kurs geht’s zwar “nur” um Torverteilungen, denn beim 1×2 Wetten gibt’s noch etwas mehr zu beachten, aber er ist ein hervorragender Startpunkt.
Kennst du die beiden Artikel hier?
Tore in der Bundesliga: Abweichung vom Mittelwert & Standardabweichung
Andere Länder, andere Sitten – Tor Statistik Bundesliga, Premier League, Le Championnat & Eredivisie
Sollten deine English Kenntnisse nicht von schlechten Eltern sein, dann lege ich jedoch die englische Version ans Herz. Diese ist nicht nur wesentlich besser formatiert, sondern viele Fragen sind wesentlich detailierter beantwortet.
Ich hatte den Kurs zuerst auf Deutsch geschrieben hatte, dann hat diesen ein Übersetzer aus dem Finanzbereich übersetzt, und schließlich hat mein Mann editiert. Es ist somit das Werk dreier Leute geworden, was dem Kurs echt gut getan hat. Er ist toll wie er ist im Deutschen, aber im Englischen ist er ein Kunstwerk geworden. 🙂
welche daten sollte man bei einem aufsteiger verwenden von 25 spielen!? beispiel Hertha BSC..2013/14 —> 1.Bundesliga, 2013/12 —-> 2. Bundesliga, 2012/11 —> 1. Bundesliga
die daten von der zweiten liga oder die von der ersten liga 2012/11??
und lässt sich trotzdem das programm verwenden, wenn es kaum h2h daten gibt??
Es ist schon herausfordernd genug, einigermaßen akkurate Vorhersagen für Spiele mit einer H2H History zu erstellen, aber Spiele mit Aufsteigern… Mann oh Mann!
Man muss Riesen Portfolios an Wetten haben, so dass Durchschnittswerte der letzten Saison eine Rolle spielen.
Ich empfehle die Finger davon lassen!