
Manchmal ist es notwendig, aus einer Reihe von Wettquoten die Durchschnittswettquote zu ermitteln, welche dann als Basis für weitere Berechnungen dient, beispielsweise zur Berechnung von Abweichung und Varianz.
Vor allem, wenn man Wettquoten im europäischen Format (Dezimalzahlen) benutzt, könnte man denken, dass zur Berechnung der Durchschnittswettquote einfach nur das arithmetische Mittel der analysierenden Wettquoten gebildet wird. Dies ist jedoch ein falscher Ansatz und führt zu einem irreführenden Ergebnis.
 Bild: Elnur (Shutterstock)
Bild: Elnur (Shutterstock) Zur Erinnerung, europäische Wettquoten berechnen sich als Kehrwerte der erwarteten Wahrscheinlichkeiten der Ergebnisse:
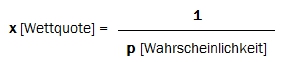
und umgekehrt… Die durch Wettquoten implizierten Wahrscheinlichkeiten berechnen sich als Kehrwerte der Wettquoten:
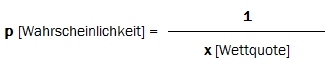
Da die Wettquoten (Merkmalsausprägungen) Verhältniszahlen darstellen, ist es falsch, das arithmetische Mittel als Maß für einen Durchschnittswert zu verwenden.
Die korrekte Herangehensweise zur Berechung einer Durchschnitsswettquote ist das Bilden des harmonischen Mittelwertes! Das harmonische Mittel stellt einen Spezialfall des arithmetischen Mittels dar, das seine Anwendung für verhältnisskalierte Merkmale findet, wobei xi ≠ 0 gelten muss.
Das harmonische Mittel ist der Kehrwert eines aus Kehrwerten berechneten arithmetischen Mittels:
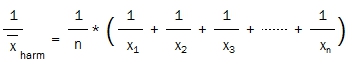
Da die Kehrwerte von Wettquoten deren Wahrscheinlichkeiten representieren, kann man das harmonische Mittel auch als Kehrwert der durchschnittlichen Wahrscheinlichkeit darstellen:
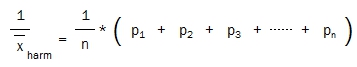
Die obigen Gleichungen umgestellt, ergibt, dass sich das harmonische Mittel berechnet, indem man n (die Anzahl der betrachteten Spiele) durch die Summe der Kehrwerte der Wettquoten (Wahrscheinlichkeiten) dividiert:
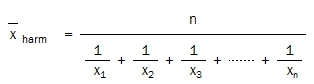
..oder, man dividiert n (die Anzahl der Spiele) durch die Summe der Wahrscheinlichkeiten:
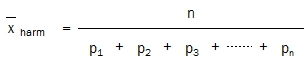
Das Ergebnis (harmonisches Mittel) ist die gesuchte Durchschnittswettquote.
In Excel nutzt man folgende Formel: = HARMITTEL(Zahl1;Zahl2;…)






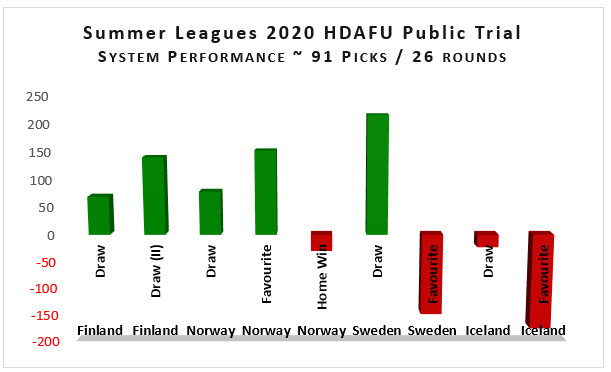
Gegenbeispiel:
Wettquoten 2,0 – 3,5 – 10,0
Arithmetisches Mittel: 5,17
Harmonisches Mittel: 3,39
Kehrwerte der Quoten – Wahrscheinlichkeiten: (50% + 28,57% + 10%)/3 = 29,5%
Umgerechnet in Wettquote: 1/29,5% = 3,39
Die beobachtete Endverteilung von Wetten dieser Art ist: 29,5%.
Es tut mir Leid, dass ich hier soviele Kommentare schreibe, aber die Sache lässt mich nicht mehr los.
Um mir die Sache anschaulicher zu machen, habe ich das Ganze auf ein Beispiel angewendet:
Drei Wettquoten – 1,5; 2,5; 3,5. Das harmonische Mittel ergibt rund 2,2; das arithmetische Mittel 2,5.
Angenommen, ich spiele jede der Wetten mit einer Einheit an Einsatz und gewinne alle Wetten. Das ergibt einen Gesamtgewinn (im Sinne von Überschuss) von 4,5 Einheiten, bei 3 Einheiten Gesamteinsatz. Mein logischer Schluss wäre jetzt, dass das arithmetische Mittel das richtige ist, da es ja bei Anwendung auf den Gesamteinsatz eben den Gesamtgewinn von 4,5 Einheiten ergibt (3 * 2,5 – 3 = 4,5). Wo liegt mein Denkfehler?
Okay, ich hab’s nochmal durchdacht, und jetzt bin ich völlig verwirrt. Wahscheinlichkeiten sind Verhältniszahlen, das macht Sinn. In dem Artikel von mathebibel steht nun aber, dass das harmonische Mittel zum Einsatz kommt eben bei der Ermittlung des Mittels von Verhältniszahlen. Demnach müsste es doch eigenltich umgekehrt sein, und man würde das harmonische Mittel der Wharscheinlichkeiten errechnen. Oder, man dividiert n (die Anzahl der Spiele) durch die Summe der Wettquoten. Ist der Artikel fehlerhaft, liegt hier ein Spezialfall vor, oder bin ich einfach nur gerade ein bisschen blöd?
Okay, ich bin auch alles andere als ein Experte auf dem Gebiet. Dachte nur, da hätte sich vielleicht ein kleiner „Ausdrucksfehler“ eingeschlichen.
Hallo Soccerwidow,
du schreibst „Das harmonische Mittel stellt einen Spezialfall des arithmetischen Mittels dar, das seine Anwendung für verhältnisskalierte Merkmale findet, …“ – Ich bin aber der Meinung das „verhältnisskaliert“ hier das falsche und irreführende Wort ist. Die Verhältnisskala beschreibt das höchste metrische Messniveau und beeinhaltet somit Variablen wie Gewinn/Verlust – wovon sich natürlich das arithmetische Mittel bilden lässt.
„Das harmonische Mittel kommt meist dann zum Einsatz, wenn der Mittelwert von Verhältniszahlen gesucht ist. Eine Verhältniszahl ist als Quotient zweier statistischer Größen definiert.“ – mathebibel.de/harmonisches-mittel
Also wohl eher Verhältniszahlen anstatt verhältnisskalierte Merkmale.
LG Max
Wettquoten sind keine Verhältniszahlen, deren Kehrwert (Wahrscheinlichkeiten) jedoch ja. Von denen bildet man dann ja auch das arithmetische Mittel, und bildet dann wieder den Kehrwert, um zur Wettquote zurückzukommen.
Keine Sorge, der Artikel ist mathematisch 100% korrekt! Ich hab‘ damit sogar ein paar Uni-Mathelektoren zur Verzweiflung gebracht. 🙂
„Man wird (mit Erstaunen?) feststellen, dass der harmonische Mittelwert die tatsächlich beobachtete Verteilung der Ergebnisse widergibt.“
D.h. aber auch gleichzeitig, wenn man auf Quoten über diese harmonische Mittelwert beim Heimsieg Arsenal setzt, dann sollte „die-Strategie“ auf langer Sicht mit einem Gewinn belohnt werden, oder?